Update May 12, 2020. I rewrote this code in Fortran.
Update July 30, 2018. I just realized that it is not needed to put the recovery events on the heap (stupid me). So I took some time to seriously squeeze out most from this approach. You can find the code at the Github page below. It’s 2-3 times faster now. An N = 10,000, m = 3, BA model network takes 0.35ms / outbreak for β = 0.3.
I needed some reasonably fast C code for SIR on networks. Funny enough, I just had C code for a discrete-time version, nothing for the standard continuous-time, exponentially-distributed duration of infection. Although there are book chapters written about this that are more readable than this post (and accompanied by Python code), I decided to write my own code from scratch* for fun. This post is about some of my minor discoveries during this coding and comments to the code itself (that you can get at Github . . it is reasonably well commented and well structured, I think, and should be instructive). Probably all points are discovered before (if not, it is anyway too little to write a paper about).
*Except some old I/O routines & data structures.
What I remember from Kiss et al. ’s book is that there are two different approaches: the Gillespie algorithm (1. Generate the time to the next event. 2. Decide what the next event will be. 3. Go to 1.) and event-driven simulation (1. Pick the next event from a priority queue. 2. Put future, consequential events in the queue. 3. Go to 1.). I decided to go for the latter, using a binary heap for the priority queue. The Gillespie algorithm comes with so much book-keeping overhead that I can’t imagine it being faster? (Or are there tricks that I can’t see?)
Using a binary heap to keep track of what the next event is turned out to be very neat. It is a binary tree of events (either a node getting infected or recovering) such that the event above (the “parent”) happens sooner than a given event, and the event below occurs later. As opposed to other partially ordered data structures, it fills index 1 to N in an array. Extracting and inserting events takes a logarithmic time of the size of the heap. There are two functions to restore the partial order of a heap when it has been manipulated—heapify-down for cases when a parent-event might happen later than its children, or heapify-up when a child event might happen sooner than its parent. Heapify-up is faster (briefly because one child has one parent, but one parent has two children). Anyways, here’s the pseudo-code for one outbreak (with a Python accent):
initialize all nodes to susceptible get a random source node i insert the infection event of i (at time zero) into the heap while the heap is not empty: i := root of heap (the smallest element) if i is infected: mark i as recovered move the last element of the heap to the root heapify-down from the root else: [1] mark i infected add an exponential random number to i’s event time heapify-down from i for susceptible neighbors j of i: get a candidate infection time t (exponentially distributed + current time) if t is earlier than i’s recovery time and j’s current infection time: if j is not on the heap: add it to the end of the heap update the infection time and heapify-up from j [2]
Comments:
[1] i has to be susceptible here, it can’t be in the recovered state
[2] since this update can only make j’s next event time earlier, we can use heapify-up
I’m too lazy to make a full analysis of the running time. For an infection rate twice the recovery rate, it runs 3000 outbreaks / second on the (16000+ node) Brazilian prostitution data (the naïve projection of the original temporal network to a static graph) on my old iMac.
The greatest joy to code this is, of course, to conclude it matches theory. I will show tests for 10^7 averages of a graph that, although small, has a very complex behavior with respect to the SIR model and thus is a good test case.
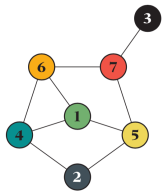
(In general, the most useful graphs for testing are complex enough for as many rare situations as possible to occur but small enough for signals from inconsistencies not to be drowned out by the rest of the network. Of course, you should (and I did) test different sizes.) For this graph, the expected outbreak size as a function of the infection rate x (assuming unity recovery rate) is exactly:
(1176*x^10+8540*x^9+26602*x^8+45169*x^7+46691*x^6+31573*x^5+14585*x^4+4637*x^3+977*x^2+123*x+7)/(168*x^10+1316*x^9+4578*x^8+9303*x^7+12215*x^6+10815*x^5+6531*x^4+2653*x^3+693*x^2+105*x+7)
The expression for the extinction time is much hairier:
(442496313262080000*x^40+27309066273423360000*x^39+807198400365952204800*x^38+15233070453900950384640*x^37+206427866398963479221760*x^36+2141932153788541338545664*x^35+17719320539717791500394656*x^34+120145769873280118142644464*x^33+681221206915024428485214000*x^32+3278911649316279397579655592*x^31+13554787582943216410512697434*x^30+48569821774947667173936604439*x^29+151963565615908045852605675638*x^28+417620288351605943926948229650*x^27+1012913280691378553984324143722*x^26+2176667408304962785107092061516*x^25+4157092031905378007476598228216*x^24+7073442188135283053895848231147*x^23+10743225033192917534525947880090*x^22+14584763731408596387436152087998*x^21+17714128509371287214419052953854*x^20+19257405578330410279734245444259*x^19+18738999678496655861828124214978*x^18+16315016288984176996492958607395*x^17+12698218026033692726424039694292*x^16+8823022276481055524449635661812*x^15+5462291880609485517543478166640*x^14+3005395264581878748317260429008*x^13+1464727118944592924512790487840*x^12+629657756169020017716116405376*x^11+237476658442269627398737860480*x^10+78048239230716482170978064640*x^9+22160762757395228067305587200*x^8+5376057161802601164632755200*x^7+1098215019757225723412736000*x^6+185258719580642643530649600*x^5+25115058278113706735616000*x^4+2629123086644412825600000*x^3+199399626889150464000000*x^2+9746072724455424000000*x+230390642442240000000)/(170659735142400000*x^40+10552460289638400000*x^39+312579991642963968000*x^38+5913391930417107763200*x^37+80362252019181365452800*x^36+836621475718722798182400*x^35+6948018151443087351091200*x^34+47327942978266352806656000*x^33+269810018795323799022182400*x^32+1307052538762076026520947200*x^31+5444452286343916086307449600*x^30+19683669375201197705776214400*x^29+62231912003456916355167472800*x^28+173109171912478541298715766400*x^27+425771864044847276704261819200*x^26+929669399656909987558520318400*x^25+1807917786488039546732408136000*x^24+3139331989062859723657121976000*x^23+4877014303846459457641565208000*x^22+6788014157540072132528114808000*x^21+8472216170656876854464167248000*x^20+9486363482241793767946469304000*x^19+9528536552497805862221968584000*x^18+8581068060934417967679452596800*x^17+6921355213421644368330335851200*x^16+4992142541382466682646297729600*x^15+3212789089879422999417773044800*x^14+1839664938944855009388405816000*x^13+933857320832833507287930597600*x^12+418340350779697721246663332800*x^11+164443976238518260207100150400*x^10+56319814910560911233147769600*x^9+16656366857169290147296243200*x^8+4205657447804826471220761600*x^7+893320008645089363572684800*x^6+156509988918986684124057600*x^5+22007772093708244924416000*x^4+2386316399921414553600000*x^3+187194956880347136000000*x^2+9449856184172544000000*x+230390642442240000000)
(How to calculate these expressions is the topic of this paper.) Anyway, they did immediately match perfectly (usually, plotting any consistency check like this sends me into another round of debugging):


All in all, it was a fun coding project (and quick—about 2 hr of primary coding and 3 hr of debugging . . no profiling or fine-tuning). Now let’s see if I can get some science done with it 😛
Without thinking too deeply, it might not be so straightforward to modify this code to the SIS model. It could be that one event changes many other events in the heap, which would make an event-based approach slow. In general, SIS is a much nastier model to study (computationally) than SIR. Both because it can virtually run forever, and that the fact that generations of the disease become mixed up prevents many simplifications (e.g., when calculating probabilities of infection trees).
Finally, the title of this post is, of course, a wink to FFTW (Fastest Fourier Transform in the West). I’m not sure this is the fastest code publicly available, but it shouldn’t be too far from it?
Hi, Peter, my name’s Yangyang.
I’ve read your post in detail. It is indeed a very effective program to implement the SIR. And I also read the source code of EON package developed by Kiss et al following your instruction in the post. I found there are some difference on implementing the FastSIR function.
Particularly, when go through the neighbors of an infected node, in your code, as following:
for susceptible neighbors j of i:
get a candidate infection time t (exponentially distributed + current time)
However, in Kiss et al’s version, to get the infection time of neighbors, it is a little complicated yet understandable:
Firstly, it gets the infected node i’s duration time period t1 from exponentially distribution.
Secondly, it calculates the transmission probability p during time period t1, p=1-exp(-tau*t1).
Thirdly, sampling from his n neighbors using binormal distribution p to determine m transmission events. Finally, in each transmission event, the neighbor node will get an infection time: current time + exponentially distributed truncated by t1.
Well, your code is obviously more effective and concise. However it is also less straightforward. For a rookie in this filed like me, I have difficulties understanding the equivalence of these two implementations.
I guess the event in the Kiss et al’s version is the transmission event for each edge. and in your version, the event is state change for each node. if I am right, are these two simulation process still equivalent?
I’ll appreciate that if you can explain for me in more detail.
Thanks,
Yangyang.
LikeLike
I wrote my code from scratch after learning the ideas from Kiss et al.
There is no need for calculating a transmission probability and my code doesn’t. You can calculate the time until a node would infect its neighbor *provided it is still infectious* and if it the infection time happens after it gets recovered then no contagion happens. This is checked at the line
if ((t < n[me].time) && (t < n[you].time))
in my code.
LikeLike
Thanks a lot, I got it.😁
LikeLiked by 1 person
Hi Peter, I wrote a FastSIR code written in Julia, which appears to match your implementation. I plan to look into temporal networks next. I was wondering whether anybody considered a fast version of SEIR along the same lines. Given that S -> E is similar to S -> I in a SIR, and E->I and I->R only depend on the node itself, shouldn’t a fast implementation be straightforward? Thanks. Gordon.
LikeLike
Hello Gordon! Thanks for your interest in my code. You could definitely use the same type of algorithm (event-driven algorithms in the terminology of Kiss, Miller, Simon https://www.springer.com/gp/book/9783319508047 ) It would be a little less elegant though—because you need variables explicitly representing the state of each node (at least if they are E or I). Also, the heap would contain both S->E and E->I events. Still, I think such an approach would be faster than a Gillespie type algorithm for SEIR.
LikeLike
Thanks for the reply, Peter! These fast algorithms are all relatively new to me. I agree that elegance decreases. Correct me if I am mistaken, but the cost of the algorithm is in the scan through the neighbors, which is not necessary for the E -> I transition. Why is it you think that SEIR has been far less studied? Is it because it is not as amenable to theoretical approaches? I was also wondering if there would be a way to use two heaps for fastSEIR: one for S->E and one for E->I for increased efficiency. Of course, the more states there are, the more convoluted a fast algorithm is likely to become.
LikeLike
SEIR is probably less studied because it is more complicated and in many respects but still behaves like SIR. In the trade-off between simplicity and accuracy, many researchers think SIR is a better deal.
In the SIR code, we don’t need an explicit variable for the state. One can infer it from the time and the heap index, but that would be needed for SEIR (so it get more complicated than expected from just adding a variable . . I think). Maybe I’ll make an SEIR version some time. I think it is easier to think about algorithms when one is actually writing actual code.
LikeLike
I have one last comment. In your sir.c code, you do not appear to have a recovery rate. The time to infection and the time to recovery both seem to be a function of the transmission rate \beta. Why is that? In my own code, I treat recovery rates and transmission rates as separate variables.
LikeLike
SIR on static networks is effectively a one-parameter model. One way of thinking about it is that all quantities of dimension time are measured in units of 1/(recovery rate). If you calculate e.g. the average time to peak prevalence with nu = 0.5 / day then you have to multiply the output time by 2 to get the answer in days.
SIR on temporal networks (since you mentioned it) is truly a two-parameter model.
LikeLike