In this blog post, I will explore why network science is mostly a science of large networks and argue that studying small networks can be just as rewarding and challenging as studying large ones. In other words, a manifesto for small-network science. (But a modest one, because it is not going to be any main research direction for me.)
As a Ph.D. student in statistical physics who wanted to do interdisciplinary science, P. W. Anderson’s essay “More is different” was my battle hymn. Anderson argues that most branches of science are concerned with emergent properties of interactions between many units described by another branch of science, lower in a hierarchy. Social science phenomena emerge from psychological phenomena like solid-state physics emerge from particle physics. The emergent phenomena are so different from their constituents’ intrinsic features that lower-level science is useless to describe them. More units from one science make something so different that it becomes another science—i.e., more is different.
Many of Anderson’s examples come from the physics of phase transitions, and since that was my thesis topic (before I changed to networks), I felt well equipped to go out and do interdisciplinary science. The recipe was simply: take interactions from psychology, let N → ∞, and get social science, etc. Easy! Or, so I thought until my sociology colleague tossed me a copy of Schelling’s Micromotives and Macrobehavior. The study of emergent phenomena, I realized, was already present throughout the hierarchy of science and the specific concepts and skills statistical physicists have—to characterize phase transitions—would maybe not be so useful after all. Even if I could whip up a model of a social system and get a critical exponent, clearly no sociologist would care. It wouldn’t say anything about society, and it wouldn’t even be empirically measurable. Yet though physics has tools and ideas worth exporting, every type of micro-to-macro transition ultimately needs its own concepts and skills (which is something Anderson alluded to as well).
When I started studying networks, I had a strong sense of a connection between networks and emergent phenomena. Perhaps because the networks that we investigate are so large that infinity doesn’t seem that far away. Probably because the Santa Fe Institute has been a hub for both networks and emergent phenomena. However, emergent behavior in networks (or rather, the network science literature) typically happens for dynamic systems on the networks rather than the networks themselves. There are some prominent exceptions, such as scale-free degree distributions. But that type of emergence is somewhat different from the physical systems Anderson had in mind since it does not involve any symmetry breaking, or divergent correlation lengths, as phase transitions in physics do. All in all, emergent phenomena came to play a smaller role in my own (and others’) network science than I thought it would around 2005.
Rather than referring to emergent phenomena, the usual motivation for network science as a science of large networks is instead in line with data science. To quote myself: “To understand how large connected systems works, one needs to zoom out and view them from a distance. In other words, one needs a principled, consistent way of discarding irrelevant information. A common way of doing this is to represent the system as a network, where nodes are connected if they interact.” As the narrative goes: For tiny graphs, one can get a lot of insight from just plotting them. The challenge comes when the networks reach thousands of nodes and beyond. That requires fast algorithms and many times, new ways of thinking as methods developed for small networks sometimes fail to make sense. Take component size vitality, for example—an exquisite measure that captures the impact of deleting a node i. It is defined as (S(G) – 1) / S(G – {i}), where S(G) is the size of the largest component of G, and the denominator contains G with the node i deleted. This measure works very well in small, sparse graphs. It coincides with the impact on disease spreading of vaccinating a person in the limit of high contagiousness. However, for larger and denser networks, it will always be very close to one and thus not so insightful (just like vaccinating one person would not stop any disease).
The above example tells us that methods designed for small graphs can fail for large ones. But we can also turn it around—component size vitality is a good quantity for small graphs, and since real networks are sometimes small, doesn’t this mean that we need a network science for them too? Large networks are usually more challenging for algorithm design, but this does not have to say small networks are easier to understand. For another example, consider the prisoner’s dilemma game with agents following the strategies of the highest-scoring neighbor on everyone’s favorite karate club network. If one drives the dynamics by occasional mutations (agents following a random strategy), then the state of cooperators and defectors will occasionally jump between two configurations:

This phenomenon turns out to depend, in a complicated way, on four vertices vA,B,C,D. We couldn’t figure out a general characterization of these nodes at the time, but my hunch is that there should exist one. At least they all seem to lie on the boundary between two clusters in the network . . which should be a lead to follow. In either case, this is one of many examples that small graphs may pose tough questions as well.
The large-N limit simplifies many things and is an excellent starting point for one’s explorations. But to get a more complete picture, why not also start on the other end? In a few papers (this, this, and this), we have studied dynamic systems on tiny graphs, where we have gone through all distinct, connected graphs in order of increasing size. To be able to consider all graphs instead of being confined to a graph model opens up for many new possible questions:
- What is the smallest graph with this or that property? Brandes and Hildenbrand identified the smallest graph where classical centrality concepts rank different vertices as the most central (below). We found the smallest graphs that give different nodes as the most important concerning different roles in disease spreading scenarios in this paper.

The smallest graph where the node of highest degree (D), closeness (C), and betweenness (B) are all different. - How much do constraints from a graph being connected affect the extreme values of quantities? When studying small graphs, one does not have to be restricted to graph models but can analyze all graphs. One does not have to rely on a heuristic algorithm to find the extreme graphs. Many extreme values are trivial, but not all.
- Can we discover patterns in the exact solutions of dynamic systems on graphs? For small graphs, we have the opportunity of using (computationally slow) computational algebra to derive exact solutions. From these, we can discover patterns (statistical laws) in a similar way to when analyzing output from stochastic simulations or experiments.
- What is the small graph with the most complex behavior? Such a graph could be useful as a test for stochastic methods, as they both would be challenging, and small enough for simulation methods to be able to resolve the problem (by a huge number of averages). For the SIR model, the graph below has remarkably complex behavior. Measures of influence disagree on which node is most important, and that also changes many times with the model parameters:
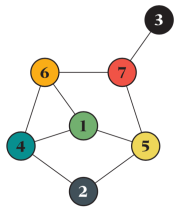
A graph with a very complex behavior with respect to the SIR model. - Are there some unexpected phenomena to be discovered? Something where the behavior in a sizeable self-averaging graph is uneventful, but the more significant influence of local counterintuitivities (like Braess’ paradox) in small graphs make a difference?
If you’re interested in this approach, the first step—to get the graphs themselves—is already done for you. There are libraries of all distinct graphs, connected or not, with sizes up to 13 vertices, and reasonably fast programs to generate even larger ones. To be able to answer “what is the smallest?” questions conclusively, you might need to solve equations algebraically. For disease-spreading models, this means you’d need fast polynomial algebra code, for which I recommend the FLINT library. Another fun thing is that you’d probably run into the famous graph isomorphism problem (which is nowhere to be seen in large-network science). I use the igraph library for that purpose. You can find my small-graph code for the SIR model here and the SIS model here.
To conclude by going back to “More is different.” Physics is a field that deals with everything from single particles to infinitely many. The in-between regime—few-body physics—has its very own set of challenges, tools, and phenomena. Perhaps because network physicists tend to come from a statistical physics background, the focus has been on the large-scale limit. But there is nothing less “physics” about small graphs. Maybe the analogy is too far-fetched, but the success of few-body physics—the discovery of Efimov resonances and the like—might bode well for small-network science.
Here’s a recent article trying to bring attention to social coordination in-between, which may be of your interest http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0193843
LikeLike
Here is a recent short essay on “scaling down” in network analysis. http://journals.sagepub.com/doi/abs/10.1177/2053951715602497 “Scaling down” is the problem of how macro-level features of Big Data affect, shape, and evoke lower-level features and processes. I identify four aspects of this problem: the extent to which findings from studies of Facebook and other Big-Data platforms apply to human behavior at the scale of church suppers and department politics where we spend much of our lives; the extent to which the mathematics of scaling might be consistent with behavioral principles; moving beyond a “universal” theory of networks to the study of variation within and between networks; and how a large social field, including its history and culture, shapes the typical representations, interactions, and strategies at local levels in a text or social network.
LikeLike
Here is a recent short essay on “scaling down” in network analysis. http://journals.sagepub.com/doi/abs/10.1177/2053951715602497 “Scaling down” is the problem of how macro-level features of Big Data affect, shape, and evoke lower-level features and processes. I identify four aspects of this problem: the extent to which findings from studies of Facebook and other Big-Data platforms apply to human behavior at the scale of church suppers and department politics where we spend much of our lives; the extent to which the mathematics of scaling might be consistent with behavioral principles; moving beyond a “universal” theory of networks to the study of variation within and between networks; and how a large social field, including its history and culture, shapes the typical representations, interactions, and strategies at local levels in a text or social network.
LikeLike